Análisis del problema

 

Analizar un problema

Numerosos autores de libros sobre programación, plantean cuatro fases para elaborar un procedimiento que realice una tarea específica. Estas fases concuerdan con las operaciones mentales descritas por Polya para resolver problemas:

1. Analizar el problema (Entender el problema)
2. Diseñar un algoritmo (Trazar un plan) 
3. Traducir el algoritmo a un lenguaje de programación (Ejecutar el plan) 
4. Depurar el programa (Revisar) 

Como se puede apreciar, hay una similitud entre las metodologías propuestas para solucionar problemas matemáticos (Clements & Meredith, 1992; Díaz, 1993;Melo, 2001; NAP, 2004) y las cuatro fases para solucionar problemas específicos de áreas diversas,mediante la programación de computadores.

 

Fase para elaborar un programa

 

 

Los programas de computador tienen como finalidad resolver problemas específicos y el primer paso consiste en definir con precisión el problema hasta lograr la mejor comprensión posible. Una forma de realizar esta actividad se basa en formular claramente el problema, especificar los resultados que se desean obtener, identificar la información disponible (datos), determinar las restricciones y definir los procesos necesarios para convertir los datos disponibles (materia prima) en la información requerida (resultados). Estas etapas coinciden parcialmente con los elementos generales que, según Schunk (1997), están presentes en todos los problemas:

1. Especificar claramente los resultados que se desean obtener (meta y submetas)
2. Identificar la información disponible (estado inicial)
3. Definir los procesos que llevan desde los datos disponibles hasta el resultado deseado (operaciones)

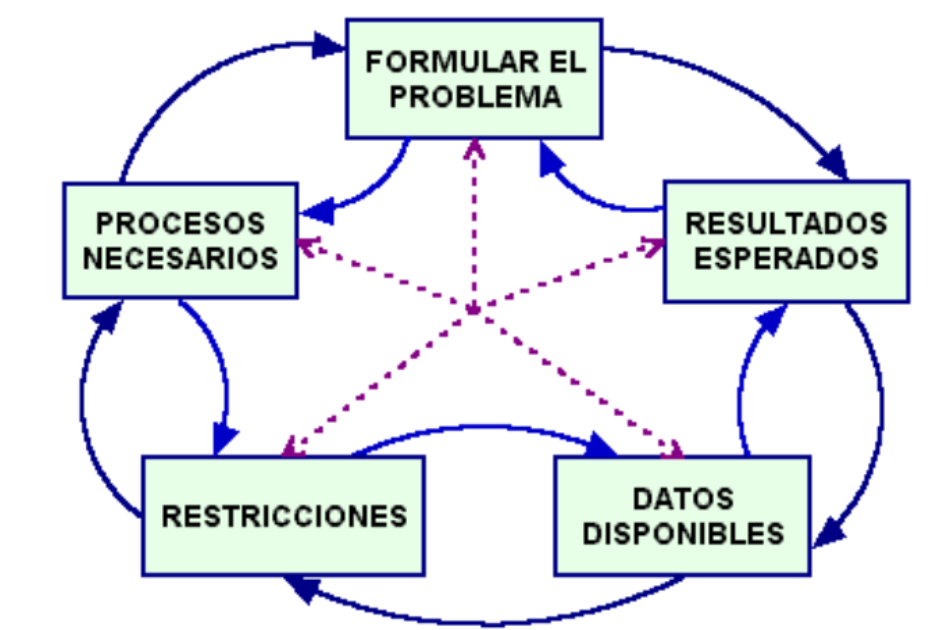
Etapas a desarrollar en la fase de análisis de un problema (entenderlo)

 

Formular el problema

 La solución de un problema debe iniciar por determinar y comprender exactamente en qué consiste ese problema. La mayoría de los problemas que se resuelven en el aula de clase llegan a manos de los estudiantes perfectamente formulados. Esta etapa es una buena oportunidad para plantear situaciones en forma verbal o escrita que vinculen la enseñanza de las matemáticas con el entorno en el que vive el estudiante y que tengan una variedad de estructuras y de formas de solución(Zemelman, Daniels & Hayde, 1998). Esta metodología obliga al estudiante a formular el problema a partir de la situación real planteada. De esta manera se contrarresta la costumbre tan común en el aula de que los problemas sean formulados por el profesor o tomados de los libros de texto (Brown & Walter, 1990).

EJEMPLO OPCIÓN 1: Juan Felipe es jefe de bodega en una fábrica de pañales desechables y sabe que la producción diaria es de 744 pañales y que en cada caja donde se empacan para la venta caben 12 pañales. ¿Cuántas cajas debe conseguir Juan Felipe para empacar los pañales fabricados en una semana?

OPCIÓN 2: Juan Felipe es jefe de bodega en una fábrica de pañales desechables y una de las tareas del día consiste en llamar al proveedor de los empaques y ordenarle la cantidad suficiente de cajas para empacar los pañales fabricados en la semana próxima. El jefe de producción le informó ayer a Juan Felipe que la producción diaria será de 744 pañales y en cada caja caben una docena de ellos. ¿Qué debe hacer Felipe? La Opción 1 plantea directamente el problema que el estudiante debe resolver. Mientras que la Opción 2 plantea una situación y la pregunta es ¿Qué debe hacer Felipe?. La Opción 2 demanda al estudiante leer muy bien el texto para comprender la situación y así poder formular el problema de Juan Felipe. Es algo similar a preguntar al estudiante “cuánto es 7 menos 3” versus preguntar “sí Rosa tiene 7 naranjas y Julio tiene 3, cuántas naranjas de más tiene Rosa”.

La comprensión lingüística del problema (entender el significado de cada enunciado) es muy importante. El estudiante debe realizar una lectura previa del problema con el fin de obtener una visión general de lo que se le pide y una segunda lectura para poder responder preguntas como:

 

• ¿Puedo definir mejor el problema? •

¿Qué palabras del problema me son desconocidas? •

¿Cuáles son las palabras clave del problema? •

¿He resuelto antes algún problema similar? •

¿Qué información es importante? •

¿Qué información puedo omitir?

 

EJEMPLO

Doña Ruby necesita decidir cómo comprar un televisor que cuesta 85000 de contado o 96000 a crédito. Ella tiene 60000 pesos en efectivo. R/. Como el efectivo que tiene doña Ruby no le alcanza para comprar el televisor de contado, ella tiene dos opciones: comprarlo totalmente a crédito o pagar una parte de contado (cuota inicial) y el resto a crédito.

Para poder resolver el problema se debe conocer el número de cuotas si desea pagarlo totalmente a crédito o conocer el número de cuotas y el valor total del televisor si se da una cuota inicial de 60000 pesos.

Precisar los resultados esperados (meta y submetas) Para establecer los resultados que se esperan (meta) es necesario identificar la información relevante, ignorar los detalles sin importancia, entender los elementos del problema y activar el esquema correcto que permita comprenderlo en su totalidad (Woolfolk, 1999).

Determinar con claridad cuál es el resultado final (producto) que debe devolver el programa es algo que ayuda a establecer la meta.

Es necesario analizar qué resultados se solicitan y qué formato deben tener esos resultados (impresos, en pantalla, diagramación, orden, etc).

 

El estudiante debe preguntarse:

• ¿Qué información me solicitan?
• ¿Qué formato debe tener esta información?

Identificar datos disponibles (estado inicial) Otro aspecto muy importante en la etapa de análisis del problema consiste en determinar cuál es la información disponible. El estudiante debe preguntarse: 

• ¿Qué información es importante?
• ¿Qué información no es relevante?
• ¿Cuáles son los datos de entrada? (conocidos)
• ¿Cuál es la incógnita?
• ¿Qué información me falta para resolver el problema? (datos desconocidos)

 

EJEMPLO Esteban está ahorrando para comprar una patineta que vale 5000 pesos. Su papá le ha dado una mesada de 500 pesos durante 7 semanas. Por lavar el auto de su tío tres veces recibió 800 pesos. Su hermano ganó 1000 pesos por hacer los mandados de su mamá y 400 por sacar a pasear el perro. ¿Esteban tiene ahorrado el dinero suficiente para comprar la patineta o aún le falta?(Adaptado de Casasbuenas & Cifuentes (1998b), página 23). R/.

Formular el problema: Ya se encuentra claramente planteado.

Resultados esperados: Si o no tiene Esteban ahorrado el dinero suficiente para comprar una patineta que vale 5000 pesos.

Datos disponibles: Los ingresos de Esteban: 500 pesos por 7 semanas + 800 pesos. Los 1000 y 400 pesos qué ganó el hermano de Esteban son irrelevantes para la solución de este problema y se pueden omitir

 

Determinar las restricciones: Resulta fundamental que los estudiantes determinen aquello que está permitido o prohibido hacer y/o utilizar para llegar a una solución. En este punto se deben exponer las necesidades y restricciones (no una propuesta de solución). El estudiante debe preguntarse:

• ¿Qué condiciones me plantea el problema?
• ¿Qué está prohibido hacer y/o utilizar?
• ¿Qué está permitido hacer y/o utilizar?
• ¿Cuáles datos puedo considerar fijos (constantes) para simplificar el problema?
• ¿Cuáles datos son variables?
• ¿Cuáles datos debo calcular?

 

Establecer procesos (operaciones) Consiste en determinar los procesos que permiten llegar a los resultados esperados a partir de los datos disponibles. El estudiante debe preguntarse: •

¿Qué procesos necesito? •

¿Qué fórmulas debo emplear? •

¿Cómo afectan las condiciones a los procesos?

• ¿Qué debo hacer?
• ¿Cuál es el orden de lo que debo hacer?

 

EJEMPLO

De acuerdo con la metodología descrita, analizar el problema de hallar el área de un triángulo rectángulo cuya Base mide 3 cm, la Altura 4 cm y la Hipotenusa 5 cm. R/ 

Formular el problema: Ya se encuentra claramente planteado.

Resultados esperados: El área de un triángulo rectángulo. 

Datos disponibles: Base, Altura, Hipotenusa, tipo de triángulo.

La incógnita es el área y todos los valores son constantes. 

El valor de la hipotenusa se puede omitir.

El estudiante debe preguntarse si sus conocimientos actuales de matemáticas le permiten resolver este problema; de no ser así, debe plantear una estrategia para obtener los conocimientos requeridos.

Determinar las restricciones: Utilizar las medidas dadas. 

Procesos necesarios: Guardar en dos variables los valores de Base y Altura; Guardar en una constante el divisor 2; aplicar la fórmula área=base*altura/2; comunicar el resultado (área).